【横山験也のちょっと一休み】№.3086
算数の手づくり教材の本を、昨年、今年と２年連続で出すことができました。
 |
 |
ヘビやサカナ、カマキリなど、一風変わったものから、単位量で出てくる２本の線分図に関することなど、あれやこれやと載っています。
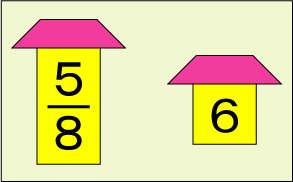
その２本の線分図ですが、「４つの数を斜めに掛けると、同数になる」というきまりがあることも、上の本の中に書いてあります。
そのきまりの大元についてまでは、本の中に書くことができませんでしたので、ここにちょっと書いていきます。
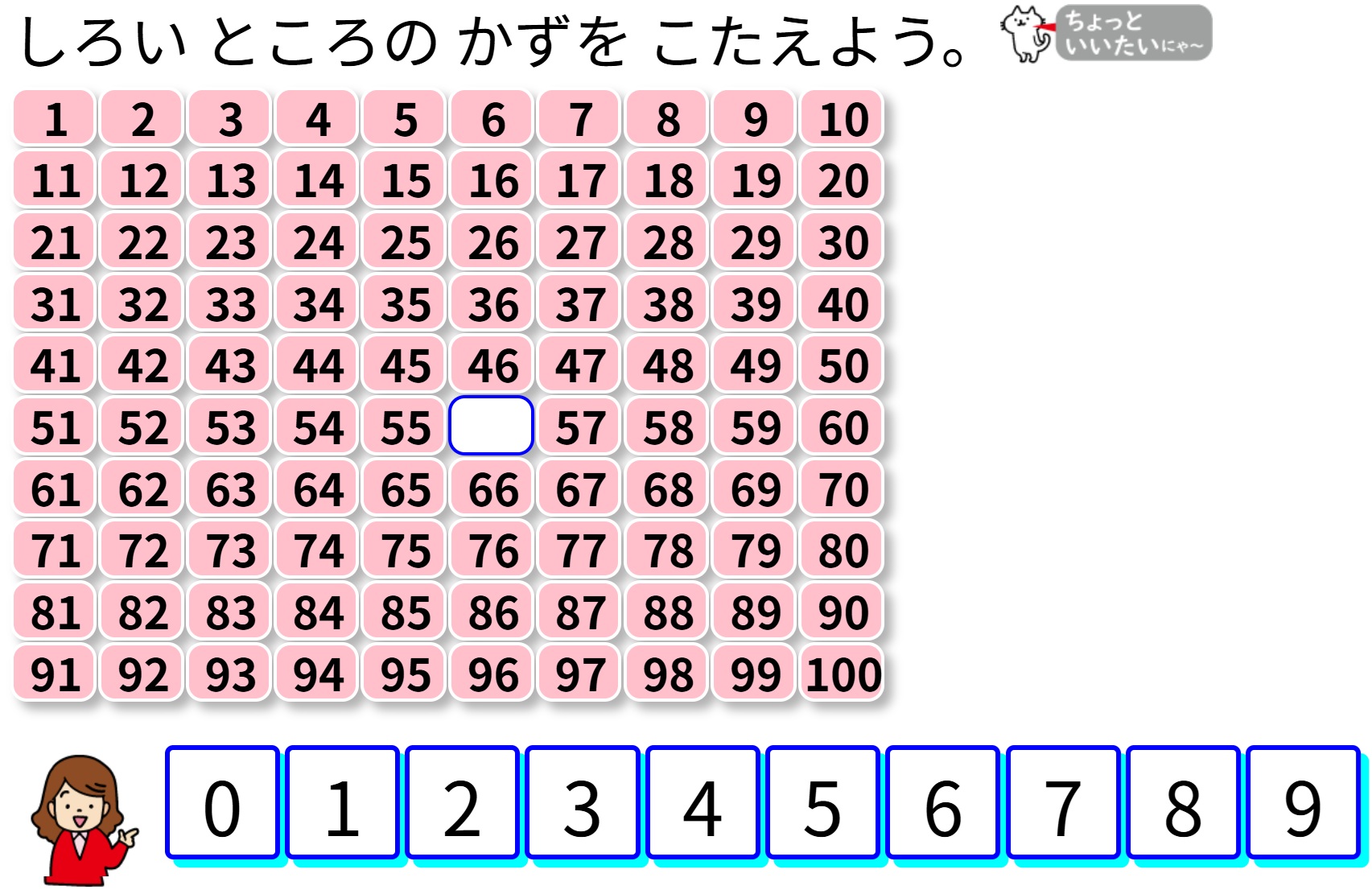
大元は２年生で登場する九九表にあります。
かけ算九九を一通り学んだ後、九九表を見ていろいろなきまりを見つける学習をします。
二次元の表ですから、基本は横にどうなっているか、縦にどうなっているかと、横と縦をしっかり見る力が付けば、学びとして十分です。
九九表の場合、斜めに連なる二乗の数を軸とした線対称の様に同数が並ぶという特殊性があります。
これを初めて知った子は、「九九表はすごい」と感じてきます。さらに、嬉しいのはそれが計算の決まりにもつながるので、九九表は一石二鳥、三鳥、四鳥･･･となる実に優れた表となります。
先の学習につながるという視点で、この九九表の中をみてみると、単位量の２本の線分図にもつながってきます。
どこでもいいのですが、「縦２ます×横２ます」をじっと見ます。焦点を絞って４つの数だけを見ると、これまでとは違うことに気が付く子もでてきます。
「斜めに掛けると、同じ数になる」と。
そこからさらに発展して、１００ます計算ならぬ、４ます計算をつくります。
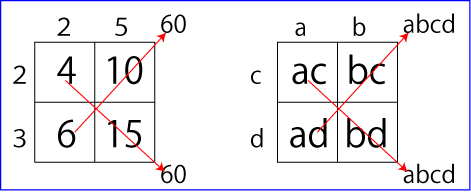すると、縦軸横軸の数が幾つになって、斜めに掛けると同数になることが、わかります。
算数は根っこの部分とあれこれつながっている学習なので、ちょっと時間がある時に、こうしたことを話すのもいい勉強になります。
—
関連記事：
