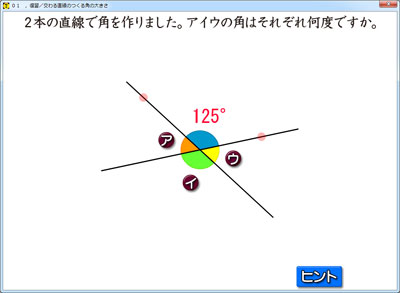
２本の直線が織りなす角度。
イは，１２５°ですね。
対頂角だからです。
アとウは，１８０－１２５＝５５なので，５５°です。
補角ですね。
この関係をつかむとき，右のような図がどこにでも出てきます。
図をそのまま使って授業をするのは，工夫力がイマイチの時です。
割り箸でも，アサガオの支柱でも，手元にある細長い棒を２本もってきて，その真ん中を輪ゴムでとめて，この図のような形を作りたくなります。
分かってもらいたい！ 楽しい雰囲気で進めたい！ そんな願いが自然と湧いてくるからです。
２本の棒は手動で動くので，その動きを見ていると，どうも「お向かいの角の開きは同じようだ」と感じ取れてきます。
動くというのは，それだけで，算数の理解をグッとよくしていきます。
授業で，この程度の工夫をしてきた先生なら，ソフトを作るに当たり，どんな風になったらいいかは，すぐにひらめきます。
１，交点を中心に２直線が動く。
これだけでも十分に良い感じです。
しかし，これだけなら棒でやった方が，教室のあちこちに持って行けるので効果が大きいように思います。
欲しくなるのは，次の機能です。
２，角度が直線の傾きに合わせて，変わる。
数で示されれば，確かに！と確信が持てます。
ここまでできるソフトであれば，授業で使った方がいいです。
算数への理解が深まるからです。
このソフトは，直線状にオレンジ色の丸があります。この丸をドラッグすると，直線がグリグリと動きます。
交点を中心に，しかも，角度が表示されて動きます。
有り難い機能です。
このソフトは，１，２の他に，ちょっとした機能を盛り込んでいます。
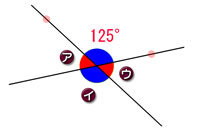
「ヒント」で，対頂角同士が同じ色になる工夫をしています。左の図のようになります。
これは，かなり強烈です。この色分けがされたまま２直線が動きます。「対頂角は等しい」とビシバシ伝わります。
角の関係が，すっかり頭に入ってしまっていたら，ちょっと背伸びをしてみるのもいいです。
ア＋１２５＝１８０
ウ＋１２５＝１８０
∴ア＝ウ
などとやると，中学の証明になります。
関係がばっちり頭に入っている子に式を使って説明することは，知的お話となり，とてもグッドです。
－－
このソフトは『子どもが夢中で手を挙げる算数の授業』の５年４巻に入っています。三角形の内角の和の学習の復習ソフトとして位置付いています。