3年生であまりのあるわり算を学習します。
その学習の一つに,わる数とあまりの関係があります。
わる数 > あまり
こういう関係があることを,子ども達にもしっかり理解してもらいます。
このような2つの数の関係は,たし算・ひき算・かけ算では,取り立てて教えることはありません。たし算で「たす数<答え」という学習は特別にはしないということです。
あまりのあるわり算で,2つの数の関係(わる数>あまり)を教えるのは,答えのミスを減らすためです。
16÷3=5あまり1 です。
これを,ちょっとした手違いで,16÷3=4あまり4 としてしまうこともあります。
教わった確かめ算をすると,3×4+4=16となり,確かめもあっています。
しかし,「4あまり4」では,×です。
あまりの4が,まだ3で割れるからです。
わり算をするということは,「もう,これ以上割れないよね」という所まで行うのがルールになっています。
このルール,あまりの無いわり算(割り切れるわり算)の時には,ほとんど自覚されません。
かけ算九九の裏返しで,エイッと答えが出るからです。
わり算はかけ算をちょっと応用した程度の計算と思い,まずは一安心します。
しかし,続けて,次なるわり算,あまりのあるわり算が登場します。
ここで,新たなルール,「もうこれ以上割れないね,という所まで割る」がでてきます。
他の計算には無い新型ルールです。
これになじむのは,なかなか大変です。
この「これ以上割れないところまで割る」というルールをしっかり自覚してもらうために,わる数とあまりの関係を知ってもらうのです。
 「あまりは,わる数より小さいんだよ」
「あまりは,わる数より小さいんだよ」
「わる数より,あまりが大きくなったら,まだ割れるって事だよ」
こう説明して,すっと分かる子もいます。
でも,分かって欲しい子は,なかなか分かってくれません。
言葉として伝わるのですが,「そうなんだ」という腑に落ちる所までなかなかたどり着かないのです。
わる数とあまりの一覧を見る経験が不足しているのです。
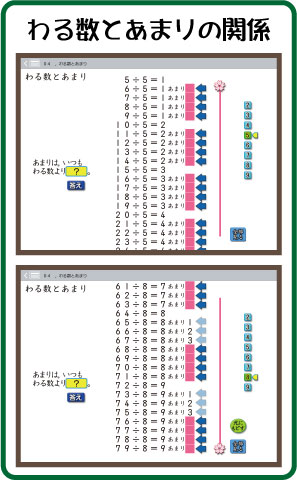
ソフト画像のように,わり算の式を並べると,あまりは1から順に数が大きくなっていると,すぐにわかります。
でも,途中まで大きくなると,突然,あまりは無くなり,また,1から順に大きくなります。
この様子を見ていくと,「÷5」のときは「4まで」,「÷8」のときは「7まで」,とその規則性に気がついてきます。
「÷3」のときは?
「÷9」のときは?
こうやって,複数のわる数の場合を見ていくことで,ようようにして,わる数とあまりの関係が把握できてきます。
「急がば,回れ」です。
言葉であっさりすまそうとするのは,急いでいる学習です。
中身がしっかりと伝わらないので,「そうなんだ」と腑に落ちない子が出てきます。
いろいろな場合を具体的に示していくことが,着実な歩みになります。
--
今回のソフトは,算数クラウドの「3年→わり算(2)あまりのあるわり算→04,わる数とあまり」です。
2の段~9の段までそろっているので,途中まで見ていく内に,みんな分かるようになったと,嬉しいお知らせを受けたことがあります。
クラウドをお使いの先生,ぜひ,子ども達に見せてあげてくださいね。
--
★3年生のわり算,算数ソフトで教室中が大盛況!
関連記事:
