３年生の文章問題「何倍の何倍」の２本目のソフトも，もっと算数サイトにアップしました。
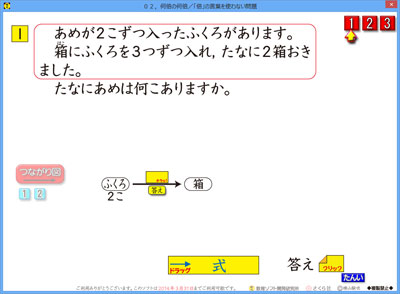
２本目は，「倍」という言葉が使われない問題です。
かけ算で何度も使ってきた「幾つ分」という言い回しや，右のような棚に２箱置いたといった言い回しがでてきます。
どの言い方も，「倍」の意味であることを理解し，そこから，「つながり図」を描いて答えを求めていこうとする考え方を学びます。
ですので，「つながり図」では，「何倍」に当たるところを問うようにしています。
－－
図をかいて問題を解いていくのですが，大事な心得は，「今回はこんな形で図をかくんだな」と，定型化してとらえることです。
形が定型化して頭に入ると，問題を見たとき，「この問題はあの時の図で解けるはず！」と頭が働きやすくなります。
この思考法は，プログラミングも同じです。
こんな動きを出したいと言うときには，そのプログラムの定型を思い出し，まずはその定型に落とし込みます。しかる後に，その時の特殊な部分を工夫して完成させます。
文章問題を解くというのは，元の文章のどこをどう図にしていくかという，「思考の動き」なのです。プログラムと同じように考えていけば，応用自在の世界がその先に待っていることもつかめてきます。
とは言っても，プログラムを知らない方には，この比喩は役に立ちませんね。
定型の典型は「式」です。
問題の意味をつかんで，式を立てるのですが，この時の形がたし算の時は＋，引き算の時は－と，形がしっかり定まっています。ですので，問題を見たときに，誰しもが何算になるかと，定型の式に当てはめようとします。
もし，式が自由なスタイルだったら，問題を読んでも思うように答えまで進めることができません。文章でダラダラ書いていくのと似たような思考になり，一気に簡単に答えを出すことができないのです。
定型化は迷いを無くし，自信を持って答えていけるための優良な思考法です。
藤本先生が，図をしっかりかける子に育てようと指導されているのは，思考ツールとして図を使う子に育て，しっかりとした力を付けさせたいと願っているからです。
図を定型化して把握させるには，図が生成される様子を数回見せることです。一つ一つ丁寧に見せることができるソフトがうってつけの教材となります。