 3年生の小数の勉強。
3年生の小数の勉強。
「0.5+0.8」なら,小数を無かったことにして,「5+8」と考えて・・・・と話し進めることもできます。
それで大丈夫な子もいますが,そうは言っても,「0.」とあるのだから,あるものを無いと考えるのはどうしても合点がいかない子もいます。
無理に考えを変えさせる必要はありません。
「仕組み(原理)」を見せ続けるのです。
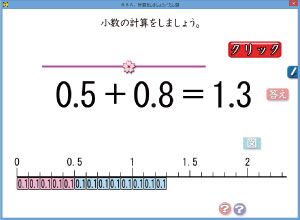
例えば,算数ソフト3年の2巻の「08A,計算をしましょう/たし算」では,数直線に0.1のカードが並びます。
0.5は0.1が5つ分。
0.8は0.1が8つ分。
だから,合わせると,1.3になるのです。
その通りのことを,その通りとして何度も何度も見せて,言葉としても「0.5は0.1が5だね」とやっていくうちに,「どうにも,このやり方は面倒だ」と感じてきます。
「もっと簡単に答えがだせるぞ!」と感づいてきます。
頭の中で小数のたし算が培養されてくるからです。
「面倒」とか「簡単なやり方」といった思考は,何度も同じことを繰り返すことにより見いだされてくる,自然な発見です。「経験的法則」とか「経験則」と呼ばれています。
誰にも備わっている,とても優れた能力です。
この「経験則」の能力を発揮させるのも,授業としては大切な方法となります。
急がずに,何度も繰り返し見せることで,「自分から発見していく」ようにすると,「算数はやっぱり面白いね!」となります。
こういう体験をさせて上げられるのが,学校の先生です。
友達の城ヶ崎滋雄先生。古武道の達人です。
「習う」ことを急ぎません。
慣れる時間を確保し,本人の内的発見が出るのを待ちます。
3年生の小数の学習でも,とても大きな成果を上げたと電話で話してくれました。
嬉しい話しだったので,ちょっと書いてみました。
