 4年生では,「概数」を学びます。
4年生では,「概数」を学びます。
「概(おおむ)ねの数」が概数ですから,平たく言うと,「およその数」となります。
ですので,概数では,たとえば,46はおよそ何十と考えることができるか,というような勉強をしていきます。
このおよそで考えるときに,重宝するのが数直線です。
数直線を見ながら,46は,およそ40なのか,およそ50なのか,どっちなのか考えるようにすると,理解が早まります。
このような学習で重要になってくる言葉は「どっちに近いか」です。
数直線は,数を長さに置き換えて表現している画期的な思考ツールです。
ですので,「およそ」という概念も「長さ」で表現することができ,それが,「近い」という言葉になるわけです。
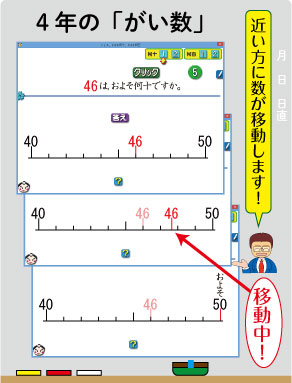
その場面のソフトが右の画像です。
『子どもが夢中で手を挙げる算数の授業』(4年5巻)に入っています。
4年の5巻には「折れ線グラフ」(ソフト数22本)も入っていますし,「分数と分数のたし算・ひき算」(ソフト数21本)のソフトも入っています。「がい数」の中にはソフトが10本入っています。上の画像のソフトはその中の「02A,およそ何十,およそ何百」というソフトです。
子ども達が,46はおよそ40なのか,およそ50なのか,予想をした後,いよいよ正解を見ます!
ちょっと,もったいを付けて「答え」ボタンにマウスを近づけます。グッと緊張感が高まります。
そんな中,「答え」ボタンが押されます。
なんと,46が動き出します!
「おー!」と声を上げる子もでてきます。
50の所に到着したら,「およそ」の文字もパッと出てきます。
画面のとおり,「46は,およそ50」とわかります。
何しろ,とても面白いので,もう一回やりたくなります。
3回,4回と問題を解く内に,「およそ何十か」という問題の答え方が分かってきます。数の移動がいつも近い方になっていると分かるからです。分かってくると,聞いてもいないのに,訳を言いたがる子が出てきます。授業が盛り上がっていく,面白い状況になります。
クリックボタンを何度押しても,ちょうど真ん中の一の位が5になる数は出題されません。
一の位が5になる問題は,緑色の「5」ボタンをクリックして,出題します。
「およその数というのは,近い方へ行く」と分かったら,いよいよちょうど真ん中の数での出題へと進みます。意見が真っ二つに分かれたら,かなり面白くなりますね。
これも,3回4回と見ていると,どうも繰り上がる方ばかりにいくことが理解できてきます。
概念がつかみにくい概数ですが,こうやってソフトを見ると,あっという間に理解が進みますね。
※昨年の暮れ,神戸の講演でこの場面を少し先生方にお見せしました。大きなどよめきが起こり,4年生担任中の先生が早速,『子どもが夢中で手を挙げる算数の授業』(4年5巻)を購入されていました。その先生のクラスでは,算数の時間は盛り上がっていると思います。良いですね。
