 平面図形の位置を見つけるソフトです。
平面図形の位置を見つけるソフトです。
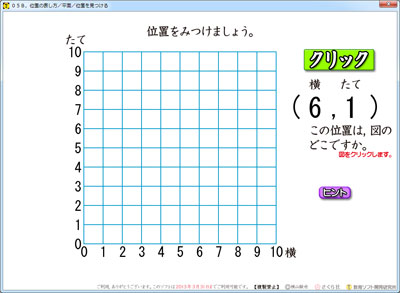
クリックをしてできた数を見て,それが座標のどこなのか,考えます。
「ここだな!」と分かったら,座標のその位置をクリックします。
正解だと,●がでてきます。
不正解だと,不正解音がなります。
こういうところは,できれば子ども達にクリックさせたい所です。
それには,ワイアレスマウス(無線マウス)があると便利です。
私自身も講演ではワイアレスマウスを使っています。それをフロアの先生方に手渡し,先生方にクリックしてもらっています。
緊張感,愉快感が断然良くなります。
ワイアレスマウスは,教室の必需品ですね。
--
ところで,平面座標の位置をなぜ「横,縦」の順に示すのでしょうか。長方形の面積のように「縦,横」としないのは,なぜでしょう。
こういう素朴なところは,なかなか教えてもらえにくいところです。
平面座標は,数直線が上下に拡張された概念なのです。
1年生の時に,10までの数や20までの数を習います。絵を伴った数直線も登場し,「数は並べて考えるんだ!」と教わります。この数直線は,100までの数で右に拡張されます。2年生で1000まで,1万までと学習し,右へ右へとどんどん拡張されていきます。
まるでアメリカの西部開拓のようでもあり,大航海時代のようにも思えてきます。
数が多くなると,表現上,横長になりすぎるので,中身の「圧縮」も行われています。
「拡張」と「圧縮」。
これは算数・数学の重要な考え方です。
「拡張」は,同様に大きくしても成り立つかな? と考える思考です。
「圧縮」は,大変だからチョー簡単に! と考える思考です。
「拡張」は冒険的な思考で,「圧縮」は面倒くさがり的思考です。
こういった人間くさいところがそのまま入り込んでいるのが算数なのです。
右へ右へと伸びた数直線。億や兆まで習うと,もう無限に右に伸びていくことが分かってしまいます。
それなら,「今度は左だ!」となるところですが,左は負の数になるので,中学までお預けです。これも,妙な話で,日常に負の数が頻繁に出る時代になっているですから,数直線を伴えば4年生ぐらいで負の数をガンガンと教えても問題ないはずなのです。
「負の数は中学から」
どうにも算数数学の都市伝説と思えてなりません。
左右への伸びが限界に来ると,突然変異的な拡張が始まります。
上下に伸びるのです。
左右とは全く質が違います。かなりぶっ飛んだ頭をしていないと,この手の拡張は生み出せません。
だから,意図的に教えていくことがとても大切となります。
上下の内,下は負の数になるので,教えるのは上にだけです。
これが,4年生で学ぶ平面座標です。
横に伸びてから上に伸びているので,これがそのまま「横,縦」という順の表記になったのです。
「突然変異的な拡張」の極めつけが,平面座標のすぐ後に登場してきます。
空間座標です。
空間座標ですから,実物を見せるのが一番良いのですが,伝達性を高めるには本などの平面上に表現します。三次元の物を二次元で表現するのですから,当然,無理が生じます。
その無理を乗り越えるのが「工夫」です。先達は縦の線を斜めに示す工夫をしました。この工夫は非常に画期的なことと,私は感動的に見ています。
空間座標のソフトも作り進める予定です。とても楽しいです。
