【横山験也のちょっと一休み】№.3726

分数の計算を学ぶと、目にする計算形式は、「分数＋分数＝？」や「分数×分数＝？」という形になっています。
こういう見方に目がしっかりと慣れているところに「分数＝単位分数＋単位分数」という出題をすると、子ども達はちょっと驚きます。

単位分数と言うのは分子が１の分数です。1/2や1/5などの分数です。
4年生で学ぶ分数は単位分数を考えの基にしています。

子ども達に単位分数を使ったどんな問題を示すかというと、例えば下のような問題です。
7/8＝１/□＋1/〇＋1/△
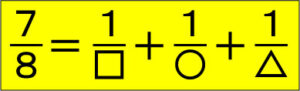分母が虫食い状態になっている単位分数が並んだ問題です。

見た目がいつもの分数の計算とは違うので、おや？と思いますが、パッと見た感じ、何だか簡単そうです。何しろ、分子が１ですから、超簡単な分数と感じられて来ます。
おっちょこちょいだった小学生の横山君がこれを見たら、「先生、こんなの簡単だよ！」と、まだ計算をする前から、さもわかったような顔をして言ってしまいそうです。
たいていはその後、恥をかき後悔となります。が、子どもの素晴らしさはそういうこともすぐに忘れて元気になることです。

普通は授業で学んだ通りに考えます。□〇△に何か数を入れてそれを通分して考え始めます。基本に忠実なやり方ですので、大いにほめるべき思考です。
ところが、この問題はそう考えるとなかなか難しいです。□〇△に簡単な数を入れて、1/2＋1/3＋１/４ではないかと想定し、通分していくと、答えは13/12となります。ちょっと大きすぎました。
ああ、これはダメだとなり、どこかの分母を大きくして・・・と考え始めます。探索への道となります。
算数の探索は大変です。わり算の商を決める時のあの状態になるからです。この問題はわり算より面倒ですので、探索で考えたのでは途中で投げ出したくなってきます。
うまくピタッと当てはまったら、それは幸運だったというだけのことです。

さあて、どう考えたらいいのでしょう。
探索以外の道となると、考え方、思考を変えなければなりません。
この問題の面白さはここにあります。
基本の考え方がダメだったら、どうするか。
この時顔を出すが、知恵と呼ばれる存在です。一種の閃きです。

しかし、その知恵もやたらと降臨してきません。
降臨はしないのですが、知恵は一度体験すると体に沁み込みやすいので、先生の方から、「実はね・・・」と話していくのもいいです。

算数の知恵の王道は図です。計算でよく出てくる図は線分図やテープ図です。それでも良いのですが、ここは「文字盤図」ですね。7/8を文字盤のようにして表すと、案外とすんなり答えが見つかります。
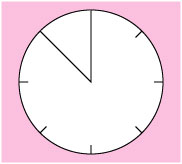さて、□と〇と△にはどんな数が入るでしょう。

答えは、□＝２、〇＝４、△＝８となります。

※この計算はエジプトの分数と呼ばれる計算です。紀元前に書かれたリンド・パピルスにこの手の問題がたくさん載っていました。

—
この３冊の本も楽しいですよ。