 小学校で習う分数のかけ算です。
小学校で習う分数のかけ算です。
この計算に取り組んだのですが、この取り組みを見て、「ムムッ!」と感じるものがある人は、きっと小学校の先生ですね。
このやり方をすると、バツになる可能性もあります。
それは、途中で約分をするのが一つのきまりのようになっているからです。
所変わって、ルワンダ。
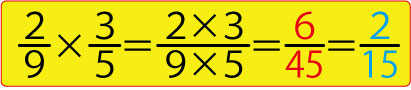
こちらでは、図のように計算をしています。
かけ算ですから、まずはかけ算をキチッと実行。
しかる後に、必要があれば約分をする、と行っています。
日本のように要領よく計算すると言うよりは、キチッと順序通りに進める感じがします。
この方法の良さは、赤いところまでにややこしい約分がないことです。
赤の所は既約分数にこそなっていませんが、正解の範囲です。
何というか、ここにちょっとした人生訓を感じます。
「まずは正解の射程範囲に入ろう!」
そういう正解エリアにいち早くインすることこそが、最も大事なことなのです。
より分かりやすい既約分数にするかどうかは、あとからゆっくり調整すればいいのです。
言うなれば、約分は誤差の範囲となります。
ところで、こういう分数の計算をプログラムする時、一番難しいところはどこだか、わかりますか。
最大公約数をプログラムで抽出する所です。
「3と9」の段階で見つけるにしろ、「6と45」の段階で見つけるにしろ、頭の中には「3だ!」と最大公約数がすぐに出てきますが、その「3」をどうやって浮かび上がらせたかのか。それを論理的に書き表す作業がプログラムなのです。
しかも、2つの数が「25と15」と変わっても、変わることのない計算式を考え出します。
へこたれそうなほど、頭を使います。
でも、一度、うまいこと計算式を見出すと、不思議と次の時は悩みが少なくなり、上達を感じます。
プログラムは論理的思考を鍛えられるのですが、どう考えたら良いかという「発想」が先に立ちます。
その「発想」の下、論理的に一つ一つ組み立てていきます。
プログラミングは論理能力も鍛えられますが、それ以上に発想力が鍛えられるありがたい世界でもあります。
算数ソフトは面白いですね。授業でドンドン使って下さい。
新しい時代の学習は使っている先生の教室から生まれてきます。
--
関連記事:
