【横山験也のちょっと一休み】№.3428
経済産業省のEdTech事業の研修、8月にスタートして昨日めでたく最終日を迎えました。
研修で私が話した内容は「さくさくドリル」と「夢中で算数」です。
「さくさくドリル」は名前の通りさくさくと取り組める楽しいデジタルドリルです。
「夢中で算数」は子どもたちに見せたくなってしまう算数ソフトです。
どちらも楽しい内容なので、私も快調に話したのですが、予想外のことも起こりました。
オンラインで話している私のWi-Fiが危なくなることが時々ありました。
ひどい時は画面共有をしたら私の回線がダウンとなってしまい、再度入室し直すこともありました。
そういうことがあっても、オンラインで話ができるのはありがたいことです。
ドリルやソフトを動かしながら、「こういう内容になっていますよ」とお伝えできるからです。
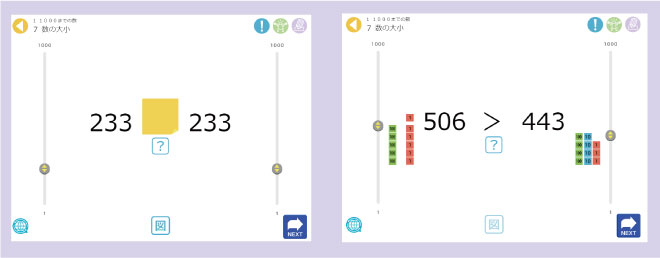
上は「夢中で算数」の中の1つのソフトです。
2年生の「1000までの数」の中にある「数の大小」を学ぶソフトです。
数を見比べるだけでなく、数カードも見せることできるので、分かりやすさが一段と高まります。
このソフトを実際に操作しながら研修でお話をしたのですが、話しながら毎度不思議な感覚になっていました。
それは不等号が大多数で、等号はたまにしか無いレアな存在だということです。
小学校の1年生から等号(=)を使って2+3=5などと勉強をするのですが、2+3>4とか2+3<7と考え始めると、不等号の場合の方が圧倒的に多くなります。小学校では、その圧倒的に多い不等号の関係になるグループをまずは考慮に入れないで、レアな存在の等号になるグループだけを先んじて学んでいます。
「2+3」と示されていると、特に問題文が無くても「=5」と答えます。問題文がある場合は、「計算をしましょう」という程度のことが書かれてるだけですが、この「計算をしましょう」をもう少し詳しく書くと、「等号の関係になる自然数を答えましょう」となります。しかし、これでは用語が難しく返ってわかりにくくなるので、「計算をしましょう」とか、それすらも略して「2+3」とだけ示すことで進んでいます。
ですので、「2+3」に対して「=6」と書いたら×になります。等号の関係なっていないからです。この時の先生は「6」に注目をしています。等号には注目しません。等号は用いると決められていると了解しているからです。
もう少し学年が進んで、不等号にも慣れ、「関係」という言葉の意味も何となく分かるぐらいになったら、「6」に注目するだけでは少々もったいなくなります。
「2+3」の後に続けて「=6」と答えを書いていたら、「<6」と直してあげるのも一つのやり方となります。実際には「等号で答えましょう」という世界観の範囲での答えなので、「<」を持ち出すことは範囲外のことになりますが、「<」を持ち出すことで、数と数の間には何らかの関係があり、「君の答えの場合は、こういう関係なんだよ」と関係(<、=、>)の見方を伝えていることになります。
こういう見方ができると、×の入る余地がなくなり、×に空しさを感じてきます。
「等号の世界観」より一段大きな「関係の世界観」へと意識が向くことは、等号を俯瞰してみるメタ思考となります。
「夢中で算数」の「数の大小」のソフトは、不等号の世界の圧倒的な量を体感できると同時に、数と数の関係を俯瞰して見ていることになります。これをスライダー操作で次々に見ることができるのですから、まさに「ソフトならではの良さ」となりますね。
なかなか面白くできたソフトと感心しています。
—
この2冊の本に載っている算数の教材アイディアが「夢中で算数」にも取り込まれています。
この2冊、面白い算数の本です。
 |
 |
—
関連記事: