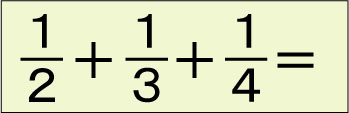【横山験也のちょっと一休み】№.2415
■古代エジプトの分数(2)■
古代エジプトの分数の続きの話です。
5枚あるパンを7人でわけるには、どうしたらいいか?
こんなタイプの問題です。
ただ、その答えは、単位分数(分子が1の分数)で表さなければなりません。
例えば、1/2枚と1/5枚などのように。
そうでないと、切ったパンを配れないからです。
例外として、2/3は使っていたそうです。
今回は、これを時計の文字盤を使って答えを導き出すお話です。
以下は私の考え付いたやり方ですので、本当の古代エジプトの人が使っていた方法かどうかは、分かりかねます。
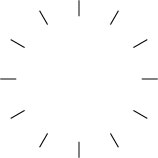 |
答を導き出すために、このような文字盤を使います。 |
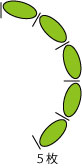 |
5枚のパンですので、文字盤の5までを使います。 分かりやすくするために、間にパンを入れてみました。このパンを7人でわけるのですが、5枚しかありません。 ですので、そのままでは分けられません。 パンは、どうしてもちぎらなければなりません。 |
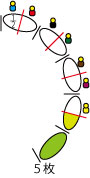 |
まずは、半分(1/2)にちぎります。 ちぎるのは、7人で分けられるところまでです。 全部切ってしまうと、ややこしくなります。4枚のパンを半分に切れば、1/2が8つで切るので、7人に配れます。半分に切るのはここでおしまいにします。半分になっている白いパンは、すぐに7人に分けてしまいます。 これで、1人が1/2枚のパンをもらいました。 残っているのは1枚と半分です。 |
| まずは、残っている1枚のパンに注目します。 1枚だけなら7人に分けるのは簡単です。 7等分すればいいだけだからです。1/7に切ったら、これも、すぐに分けます。 これで、1人分は、「1/2+1/7」になりました。 |
|
| 残っているパンは1/2枚です。 これも一塊なので、7つに分けるのはやりやすいです。 7等分すると、1/14枚の大きさとなります。 |
|
ということで、答えはこのようになります。 |
2/3が使えるので、次のようにも答えを出せます。
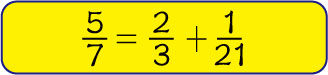
どっちが分けやすいかと言うと、今回の場合は2/3を使った方ですね。
こういう分数を知ったからと言って、現代の分数の計算ができるわけではありません。
考え方の系統が違っているからです。
古代エジプトの分数は、算数の進化の過程で絶滅をした考え方と言えます。
ですので、算数の授業で紹介するのはあまりお勧めできません。
この問題。
現代人なら、5枚のパンをそれぞれ1枚ごとに7等分して、一人一人が1/7のパンを5切れずつもらえばいいだろう、と思います。
でも、古代エジプト人はそうはしませんでした。
なぜでしょう。
疑問が残りますね。
—
関連記事: