【横山験也のちょっと一休み】№.3720
阿部先生と歓談した際、阿部先生が関孝和の話題を出してくれました。
関孝和というのは江戸時代の有名な数学者で、阿部先生が話してくれたのは関孝和の円周率・円の面積の話です。
小学校でも円の面積を学習します。円を12分割や24分割して、小さな扇形にし、それを上下で組み合わせ、平行四辺形のような形にしていきます。
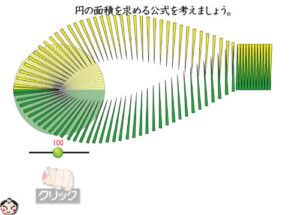
円の面積と言えば、左のソフトですね。『子どもが夢中で手を挙げる算数の授業』です!!
今も大人気で子ども達はオオッとなります。
このソフトを阿部先生も使ってくれているからか、円の面積の考え方について、阿部先生は話してくれました。
円の面積は、円に内接する正多角形の1辺の長さを求めることで近似値をつかむことができます。正多角形の辺の数をどんどん増やせば増やすほど、円周の長さに近づきます。
そういうことで、阿部先生から「横山先生、関孝和は円に内接する正多角形を、正何角形まで計算したと思いますか」と問われました。頭の中で先ほどの算数ソフトを思い出し、「100分割か200分割ぐらいかな(ソフトでは200分割まで見ることができます)」と言ったところ、「13万です」と返ってきました。まさにひえぇ~です。
その後、阿部先生から正十三万千七十二角形角形と正確に教えていただきました。『江戸時代の科学者』に載っているとのことです。
正13万角形をもし描くとなると、かなり巨大な形にしないとかけないでしょうね。関孝和、すごいです!
さて、円周や円の面積を求めることですが、大学生の時に円の面積の求め方で衝撃を受けたことがあります。
普通、
円の面積=半径×半径×3.14
で求めます。
ところが、大学生の時に神田の古本屋や国立国会図書館で収集した和算の本の中に、驚きの考え方が載っていたのです。
その式を今風の公式にすると、下のようになります。
江戸時代:円の面積=直径×直径×積率(0.78だったか?)
小学生の時からずっと「半径×半径×円周率」だったので、これ以外には無いものと思っていました。ですので、私には衝撃的な求め方で、それを卒論にも書いたほどでした。
衝撃が大きかったために、そこからあれこれ考えました。
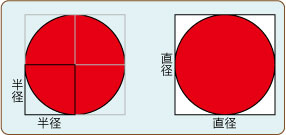
円の面積は正方形(直径×直径)の0.8倍ぐらいとした方が、感覚的に理解しやすいなぁと思ったのです。
半径の正方形だと3倍ぐらいだなぁとなるのですが、パッと見た感じで「確かに!」とは思えません。頭の中で少々ウジャウジャする感じがしてきます。3倍を説明するために何かしらのことを言わなければならない感じがしてきます。
ところが、直径の方だと、正方形の8割ぐらいと感じ取ることができます。直感的に把握しやすいです。
この直径というのは、その昔「差し渡し」と呼んでいました。この言葉は風土記にも出てきます。井戸の大きさを言い表すときに、差し渡しが何尺とか記されています。
井戸は「井」の字からすると、四角だったような気がしますが、「丸太をくりぬいて地中に埋めた井戸が、弥生 (やよい) 時代の遺跡からみつかっている」(『日本大百科全書』)とあるように、丸い形をしたものもありました。その差し渡し(直径)を記録していました。
実際の生活では半径より直径の方が測りやすかったのです。
井戸の端で棒状の物差しの端を押さえ、反対側の端にあてれば、一番長いところが直径とわかります。物差しで測ったのか、紐で測ったのかはわかりませんが、直径は実に簡単にわかります。
思うに、昔はすぐにわかる直径を基準として表現が進んだのでしょう。生活での行為に思考の基準があったように思います。(これはまた別の問題となり、実に面白いです)
また、円の面積が正方形(直径×直径)の0.8倍ぐらいということが分かっていると、折り紙に円を描いて切り抜くと、0.2が無駄になることもすぐにわかります。無駄の計算もすぐにできるのはなかなか良い感じです。
感覚的な公式なので生活密着度は抜群にいいです。
円の面積を学習して、しっかり定着をした後に、江戸時代の面積の求め方を話したこともありました。もう遠い昔のことです。
—
下の3冊の本には算数の楽しいアイディア教材が載っています。
 |
 |
 |
