【横山験也のちょっと一休み】№.3746

藤森良蔵の本に分数のたし算の問題とその考え方が出ていました。
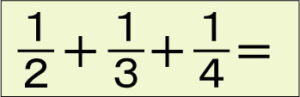この問題を見ると、たいていは２と３と４の最小公倍数（１２）を考え通分して解いていきます。それも順当ないい方法なのですが、藤森良蔵は２種類の解き方を提案しています。

１つ目は、３つまとめて計算するのではなく、出て来た順に「1/2+1/3」を計算し、その答えに１/４を足す方法を示しています。
３つまとめて通分するより、２つずつの通分の方が手堅く、間違えが生じにくいという考え方です。

また、もう一つの方法は、２つの分数をたすのなら、1/2+1/4をまず計算して、それから1/3を足しましょう、というやり方です。これは２と４には共通の約数があるので、分母が大きくならなくてすみます。計算しやすくなります。

こういった間違えずに手堅くしっかりと計算させていく導きは実にいいです。

私がこの部分を読み、特に注目をしたのは、複数の方法を示していることです。これはうっかりミスを減らす有効な方法だからです。

例えば、同じ約数を持つペアを見つけて計算しましょうというのは、あせって計算するのを防ぐ効果があります。どう計算したら素早く正しく計算結果を出せるかと考えているからです。すぐに取り組まず、まずは冷静になってアプローチを考えるため、いわゆるうっかりミスを生じにくい心構えになっているのです。
いろいろな方法を知っていることは、冷静さを生み出す原動力とも言えます。
もし、１つの方法しか知らないと、とにかくどんどんやるようになります。気が付かないままうっかりミスがちらりほらりと出てきてしまいます。

藤森良蔵がいろいろな解法を示しているのは、まずは冷静になって、どう取り組んだらよいかを少し考えてから取り組もうという、ミスを減らす実に優れたやり方なのです。

さて、少し話は変わりますが、これらのやり方とは別に、この1/2,1/3,1/4を見た瞬間に、この３つの分母はすべて１２の約数と分かる人もいます。そういう人は時計の文字盤を頭に浮かべて、特に通分をすることも無く、13/12が答えだと言い当ててしまいます。
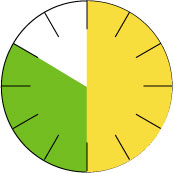オレンジが1/2で、グリーンが1/3。これに1/4（つまり、目盛り３つ分）を足したら、13/12と分かります。
一緒にいた人から、「鉛筆も使わずにどうやって計算したんだ！」と、まるで魔法のような思考と思われてしまうかもしれません。

同じ算数でも時代によって求められていることが違うのですが、よく吟味すると理にかなった素晴らしい内容と分かります。
—
私の書いた本です。面白い算数がたくさん載っています。