【横山験也のちょっと一休み】№.3517
0~12までの数字を、ABCの3つのコーナーに振り分けました。
A:0、3、6、8、
B:2、5、9、10、12、
C:1、4、7、11、
ここで、問題です。
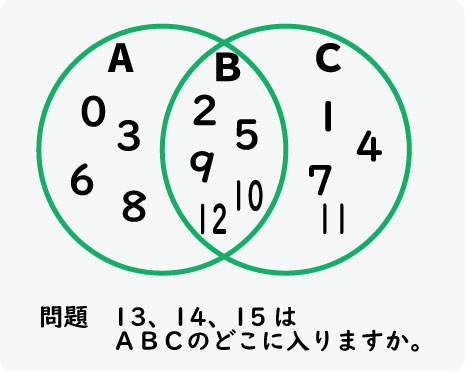
この先、13、14、15を振り分けたいのですが、それぞれABCのどのコーナーに入りますか。
————
何らかの振り分けのルールがあるのですが、それがなかなかつかめません。
つかめないのは当然で、これは「とんち」問題なのです。
振り分けのルールは、
Aは曲線でできた数の集まり。
Cは直線でできた数の集まり。
BはAC両方の性質をもった数の集まり。
となっています。
このとんち問題。
算数とのかかわりと言えば、「線には直線と曲線がある」という学習となります。
アフリカのルワンダでは2年生あたりで直線・曲線を学びますが、日本の算数では曲線を学びません。きっと、曲線を学んでもその先の学習につながりにくいので、触れないでいるのだと思います。
ですので、日本の算数という視点では、学ぶべき点がないのが、この問題です。
でも、「面白そう!」と思う先生もいて、あの子が喜びそうと思える子が頭に浮かぶことがあります。
そんな時には、ベン図を使って出題すると、見た目が算数っぽくなってきます。
見た目だけでなく、ベン図を使うことで、頭の働きが数理的になります。
ところで、この問題、ちょっとした面白さを持っています。
算数が得意な子は、数の性質をあれこれ考えはじめるので、正解になかなかたどりつけません。たどり着けませんが、数の性質を考えることで、いい勉強になります。
算数はイマイチでも、頭をひねるのが好きな子は、意外にも「わかった!」となります。こちらは、数の性質から遠のきますが、ベン図の問題に興味がわきます。「ベン図とんち王」とでも先生が言ってくれたら、ベン図が妙に好きになります。
たまには、こういうとんち問題を出題してみるのも、クラスの良い潤滑油になります。
この3冊は、私の算数の本です。緑の本は、明後日の金曜日が発売日です。楽しみです。
 |
 |
 |
