【横山験也のちょっと一休み】№.3590
算数の計算には、重要な法則が3つあります。
1つは、交換法則。2+3=3+2のような、数を入れ替えても答えが同じになるという決まりです。
2つ目は、結合法則。(2+3)+4=2+(3+4)と、計算する順番を変えても答えが同じになるという決まりです。
3つ目は、分配法則です。2×(3+4)=2×3+2×4と、まとめてからかけ算をしても、分けてかけ算をしても答えが同じになるという決まりです。
この中の交換法則は2年生になると登場してきます。プリントなどでも、「答えが同じになる式を線で結びましょう」という出題がなされています。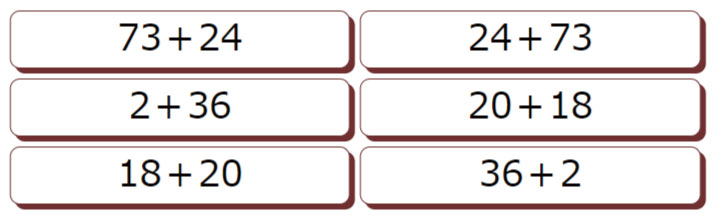
私がすごいなぁと感心することの一つがこの交換法則です。
「数を入れ替えても答えは同じ」ということが頭に入っていると、左のように6つもある式を見ても、何も計算せずに、どれとどれが同じ答えになるのか、ピタリと当てることができます。
計算なのに計算をしないのです。これはゴッドのすごさです。
そんなことを思っていると、「鬼ごっこ」などの遊びもすごい世界と感じられてきます。鬼が鬼の変装をしているわけではないのに、みんな「わーっ!」と逃げます。鬼も鬼で、どんどん追いかけます。なんで追いかけるのか、その理由はよくわかっていず、そういうルールだから追いかけているのです。
そのルールを守っているから、そこに、不思議なほどの大きな面白さが湧き上がってきます。
大人になった先生にしてみてたら、交換法則などに感動することは全くありません。でも、はじめて学ぶ子ども達には、鬼ごっこのような面白さがそこにあるのです。だからこそ、「すっげー、計算しないで分かったんだ!」と学んだルールを使っている姿に感動してあげることが、とっても大切なことになります。
 |
 |
 |
