【横山験也のちょっと一休み】№.3598
2年生で三角形や四角形を学びます。
この単元は、結構面白く、深みもあります。
真っ先に、すごいなぁと感心するのは、「三角形vs三角形もどき」「四角形vs四角形もどき」のような学習をするところです。
「三角形もどき」というのは、基本的に3種類あります。
1、角が丸まっていて、頂点が無くなっているタイプ
2、直線の一部が途切れているタイプ
3、直線が曲がっているタイプ
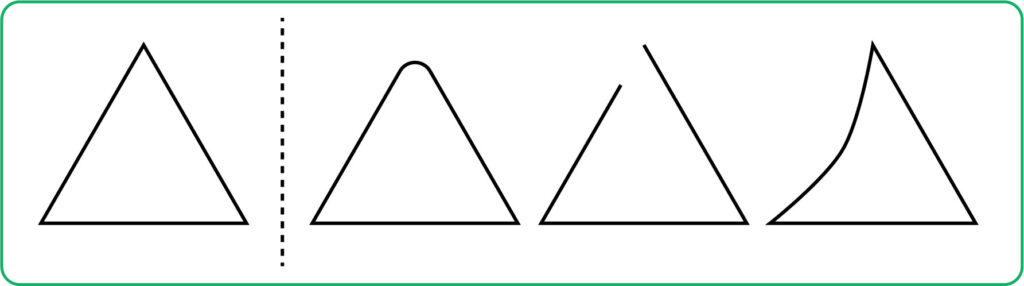
分かりやすく左に図を示したのですが、この図だけを見ていると、元の三角形1つに対して、もどきは3つあることになります。1:3ですので、もどきは元の3倍の数があるわけです。
そこからさらに考えていくと、もどきはもっともっと数が多くなります。
1のタイプのもどきは、丸め方を変えると、何通りにも形ができます。また、底角の2つの角も丸めていけば、その何倍かの数になります。非常に細かい違いまで見ていけば、無限に形があります。
2のタイプも同様です。途切れの長さを微妙に変えて、形の数をカウントすると、こちらも無限に形が存在します。
3のタイプも同様です。無限に形があります。
元の三角形1つに対して、「もどき」は無限が3タイプもあるのですから、その量は膨大です。
若いころに算数教育の本を読んでいたら、1年生で学ぶ数について、感動的な記述と出合いました。
それは、象が1頭いたら1。ねずみが1匹いたら、こちらも1。どちらも数という観点で同じと判断されます。この数で表すということは、その時点で大きさや形、色や高さや幅、重さや毛の数など、ありとあらゆる属性を無視していきます。個数以外の事をすべて捨て去って考えていくから、算数の勉強が進むのですと、そんな話が書いてありました。
これは、数以外の何かを加えて考えてみると、思考が非常にややこしくなることでわかります。例えば、象もねずみもどちらも1としては、やっぱり変だ。象は大きいのだから、「1」として、ねずみは「1」とした方が雰囲気が良く出る、などとやったらやったら、「1+1=」となり、これは2として良いかどうかわからなくなります。たぶん、「11」このようになり、結局は「象&ねずみ」としているのと変わらず、算数としての「2」にすんなりとは進めなくなります。
数での思考を進めるために、個々の具体物のもつその属性を捨て去ったのと同様に、似て非なる形を捨て去ることで、三角形や四角形が科学として思考を高めてくれるのです。
捨て去るときに大事になってくるのが「定義」です。定義をすることは、それ以外の見方を捨て去るということでもあるのです。
下の本は、私の書いた算数のアイディア教材集です。どの本もおもしろいです。
 |
 |
 |
