【横山験也のちょっと一休み】№.2985
数え棒で作った三角形の面積を2等分する問題の続きです。
左のような三角形を青い数え棒2本を使って、面積を2等分したいのです。
それには、どうしたらよいのでしょう。
と言う所で、前回、終わりました。
今日は、その続きです。
2等分ですから、目安として三角形の真ん中あたりに青数え棒を置けばよいことはわかります。
また、2本とも三角形のどこかの辺と接触することも分かります。
そんな所から、薄々こうではないかと閃いてきます。
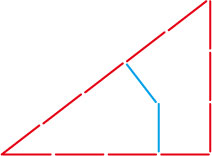この分け方は、正解です。
ですので、「さすが、よく気が付いたね」などと褒めることができます。
そうして、今回の2等分パズルの肝心なところへと進みます。
「どうして、これが2等分になるのか、ちょっと説明して」と問うようにします。
この説明がなかなかできません。
なんとなくとしか言いようがない状態になります。
けれども、ジッとよく見て考えていると、アアアッ！と気づくことがあります。
2等分した図形の中に三角形が見えてきて、そこに底辺・高さが認められると、スッキリわかってきます。
元々の三角形の面積は底辺４、高さ３ですので、
4×３÷２となり、「６平方数え棒」となります。
2等分するのですから、片方の面積は「３平方数え棒」となります。
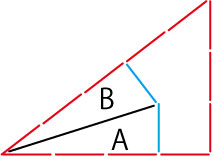
Aの部分の面積は
３×１÷２＝1.5 です。
Bも同様になるので、こちらも「1.5」です。
A＋B＝1.5＋1.5＝3 となり、ちょうど「６」の半分となります。
スッキリ、クッキリと分かるので、これを知ってしまうと、家に帰って誰かに出題したくなります。
証明が楽しくて誰かに言いたくなるのですから、これは嬉しいことです。
これも算数の持つ大きな特色と思っています。
—
関連記事：
