【横山験也のちょっと一休み】№.3109
算数のトピック的な話を一つ。
十進法と言えば、私たちが普段使っている記数法です。
０～９までの１０個の数を用います。
これがコンピュータは２進法となり、０と１だけで表現します。
二進法の２は「１０」となり、３は「１１」となります。
同様に三進法もあります。
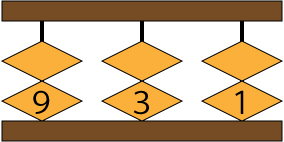三進法のそろばんをつくると、１桁に珠が２つとなります。
そこに、十進法に直した数を入れると、ご覧のようになります。
この＜１＞＜３＞＜９＞という数がなかなか面白い味を出してくれます。
＜１＞＜３＞＜９＞を上手に使うと、１～１３までの数を作ることができます。
１は＜１＞です。
３は＜３＞です。
９は＜９＞です。
ここまではそのままですから、式を必要としません。
４はどうなるかというと、＜３＞＋＜１＞です。
２は＜３＞－＜１＞とひき算をすればできます。
１０は＜９＞＋＜１＞。
このように、たし算とひき算で、残りの数をつくる式をつくれます。
さてさて、どのような式になるでしょうか。
と楽しむこともできます。
簡単ですので、チャッチャカと答えを見つけては、「できた！」の完成が上がります。
黒板に整理して書いていけば、「ほー。」となります。
念のために、残りの答えを載せておきます。
—
５は＜９＞－＜３＞－＜１＞。
６は＜９＞－＜３＞。
７は＜９＞－＜３＞＋＜１＞。
８は＜９＞－＜１＞。
１１は＜９＞＋＜３＞－＜１＞。
１２は＜９＞＋＜３＞。
１３は＜９＞＋＜３＞＋＜１＞。
—
子供達が盛り上がって時間もあったら、４桁目の数が何になるか考えさせましょう。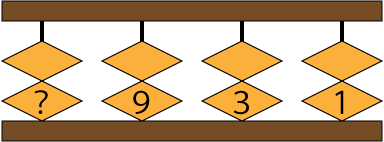
３倍ずつ増えているので、＜２７＞になります。
すると、＜１＞＜３＞＜９＞＜２７＞を使って、幾つまでの数を表せるようになるのか、推測させるのも楽しいです。
＜１＞＜３＞＜９＞が１３でしたので、
＜１＞＜３＞＜９＞＜２７＞は４０となります。
このように推測をして、４０までならたし算、ひき算を使うことで作れると見通せるのも、算数の大きなパワーです。
作れそうだと見通しが立つと、チャレンジ意欲も強くなります。
算数というのは、なかなか面白い世界を作り出してくれます。
—
このような内容は載っていませんが、下の２冊には算数の授業で使えるアイディアがたくさん載っています。
面白い本です。
 |
 |
—
関連記事：
