【横山験也のちょっと一休み】№.3581
今日も算数の話を一つ。
１年生の計算単元に「３つの数の計算」があります。
昔は「三口（みくち）の計算」と言っていました。一口（ひとくち）、二口（ふたくち）、三口（みくち）の三口です。
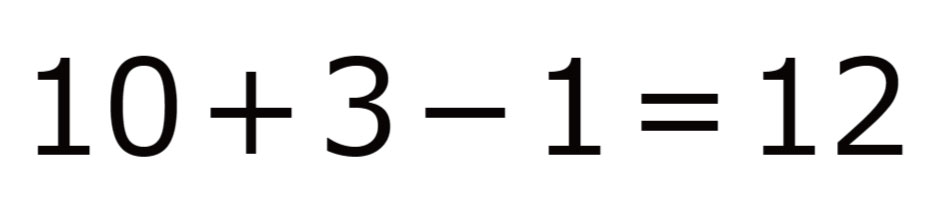昔は、二口を学んだら、それを延長して三口、四口、五口・・・と学んでいました。主に戦前の話です。
この単元でも三口の計算を学ぶので、たし算引き算は、どんどん延長しても計算できるということも学ぶ内容の一つにはなっていますが、重要な意味合いはありません。
この単元で最も重要なのは、「繰上りのあるたし算、繰り下がりのあるひき算の準備」です。
７＋５＝ この計算の準備として、
７＋３＋２＝ を勉強します。
９＋６＝ この計算の準備として、
９＋１＋５＝ を勉強します。
「１０を作って残りをたす」
このスタイルでの計算がしっかりできるようにとの配慮で存在している単元なのです。
引き算のタイプも同様です。
１２－５＝ の準備として、
１０－５＋２＝ の勉強をします。
そんなことを頭に入れておくと、指導も方向性がしっかりしてきます。
さて、プログラミングです。
算数として抑えることと、それをプログラムすることは全くの別脳です。
特にこの単元は、繰上り、繰り下がりにつながる計算とは別に、単なる三口の計算も含まれています。系統から少し外れたイレギュラーな内容も入っているということです。
こういう時は、出題を意図的に決めることができる「配列」という考え方を使います。
[9,1,3] と書いておくと、「９＋１＋３」の計算が自動的に行われるようにプログラムします。
[8,2,4]などの他に、単なる三口の計算である[3,4,1]なども含めて出題することができます。
算数もプログラムも実に面白い世界です。