【横山験也のちょっと一休み】№.3686

５年生で最小公倍数や最大公約数を学びます。
この学習の時に、簡単な素数を教えたことがありました。

教えたのは、算数好きの先生にはとても有名な「エラトステネスの篩ふるい」です。

エラトステネスというのは、人の名前です。紀元前に活躍をした偉大な学者です。
このエラトステネスは、素数を見つける方法を編み出しました。
かけ算を使って合成数（素数で無い数）をどんどん消しく方法です。

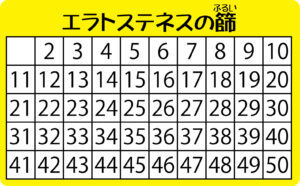
下のように、１を除いた数表をつくり、２の倍数（４，６，８・・・）に×を付け、それが終わったら、３の倍数（６，９・・・）に×を付け・・・と順にやっていきます。

そうすると、下のように数が残ります。それが素数です。

かけ算をしながらどんどん×を付けていく単純な活動ですが、子ども達は結構喜んでやっていました。

そうして、素数が見つかったところで、２０までの素数。つまり、よく使う素数を一覧にしたものを子ども達に配っていました。
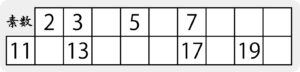２，３，５，７・・・と素数を唱えることも少ししましたが、この一覧を見て、位置を焼き付けるのも面白いだろうと思い、作ったものでした。

私が若いころにやっていたことですが、今は素数が全く顔を出さないので、こういうことは特に知る必要もありません。

時代が変わり、素数が扱われなくなるとは思ってもいなかった当時の私は、「何かを見つける方法を発見することは、歴史的な偉業となることがあるんだ！」と熱く語っていました。
教師が熱く語ることは、大切なことだ！とも思っていました。

下の３冊の本には、楽しい算数のアイディアが満載されています。