中学1年生で「正の数・負の数」を学びます。
概念としてなかなか難しいのが「負の数」です。
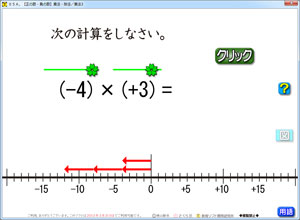
たとえば,右のソフト画面の「(-4)×(+3)」は,どう考えたらよいのでしょう。
紀元前の大数学者ディオファントスは,方程式を解いて答えが負の数になる場合は,答えがないと考えていました。代数学の父と呼ばれる偉大な数学者ですが,負の数は理解が困難だったのです。
「(-4)×(+3)」を,小学校的な言い回しにすると,「1つ(-4)の物が,(+3)ずつあります」となります。
具体的な言い方になっていますが,逆にわかりにくいです。
マイナスは,物で説明するのが難しいからです。
負の数をわかりやすくしてくれたのがデカルトです。
座標で示すと負の数は,急速に把握しやすくなります。
矢印がつくと,一層わかりやすくなります。
ですので,式の意味を理解するには,式に対応した数直線での図を見せることが大切なこととなります。
一つだけでなく,幾つかの式とそれに対応した図を見せます。
すると, 生徒は生徒なりに頭が働き始めます。
どういうきまりになっているのか,きまりを見いだそうとします。
「×(+3)」は,元の数の方向に矢印が3倍されているなぁ。
「×(-3)」は,元の数と逆の方向に3倍されているなぁ。
式と図の関係から何かしらのきまりを読み取った時に,頭の中で中学生らしい「負の数への理解」が始まるのです。
この時に,理解を一層強めてくれるのが,「用語」です。
「正の数」とか,「負の数」という言葉です。
用語が使えると,
そうか,「×(正の数)」は,元の数の方向に正しく倍するのだ。
「×(負の数)」は,正しくないから,負けているから,逆の方に倍するのだ。
などと,用語に絡めて,それなりの理屈を付けやすくなります。
日本語の算数・数学用語は,その多くを漢字で表します。
その漢字の訓読みを使うことで,理解を強められる場合があります。
「垂線」の「垂」などもその一つです。「垂れる」と訓読みできると,垂線の理解が一層良くなります。
こうして理解できたら,翌日もまた式と図のつながりを見せて,理解が定着するように働きかけます。
このような理解を助ける数学ソフトの開発を,この先も進めていきたいと思っています。