野口塾ビギナーズで６年生の「縮図」がでました。
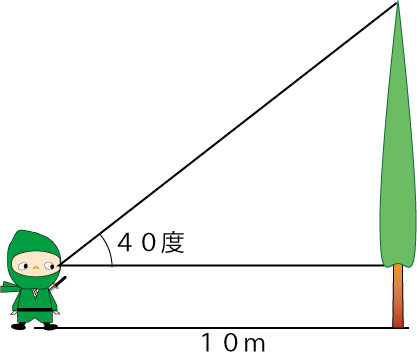
右のような図が載っていました。
１０ｍを１０ｃｍとして縮図を書き・・・と進めていくと、木の高さが求められるという学習です。
縮図を見て、そこから実際の長さを求める学習は、縮図のありがたさがわかる良い授業となります。
私も現役の時、学校の縮図を印刷し、子供達に配布して授業をしたことがあります。
学校の敷地を売りに出すとしたら、いくらになるか考えさせたのです。
事前に、学校の近所の不動産屋へ行き、学校の近くの家の土地価格が１坪いくらになっているか、調べました。
また、学校の縮図に記されていた寸法は、全部消しました。
実際の長さを図る個所をできるだけ少なくして、売値にたどり着けるか検討します。
まあ、面白かったです。
算数の単元は、「基本」と「応用」に別れています。
応用では、基本で学んだ事項のありがたさや便利さ、面白さなどが伝われば、ナイスです。
ところで、木の高さですが、これを求めるのに縮図を使うのは、ちょっと見当違いと思えます。
角度を「４０度」に設定しているのは、どう考えても、縮図を使わせるためです。
木の高さを求めるだけなら、４０度はダメでしょう。高さを求めるまでの手順が複雑だからです。
江戸時代から、角度を４５度にする、ということが伝わっています。(江戸時代には角度という概念がなかったので、二等辺の考えです。）
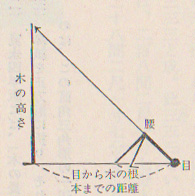
ご覧のように股ぐらから木の梢が見えると、それがちょうど４５度ぐらいになります。
多少の誤差を気にしなければ、これが一番手っ取り早いです。
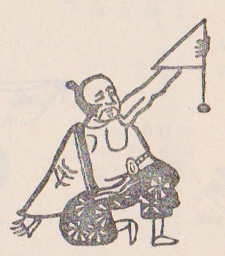もう一つは正方形の紙を半分におり、そこに重しをつるした４５度の計測器をつくります。
測る時の姿勢が重要で、片膝で座り、片手を地面に着け、上げた腕と三角形の斜辺が一致するようにします。腕で直角二等辺三角形の斜辺を作っているのです。
こういう事例は、江戸時代の算術書『塵劫記（じんこうき）』に紹介されています。
歴史的にも、基本は４５度(二等辺)とわかります。
こういう事を知っていて、その上で、ちょっと複雑になるが、実は縮図でも・・・と進むとすごい！と感じますね。
もちろん、１ｍの定規を立てて、その影の長さを測り、木の影がその長さの何個分になるかなど、各種方法はあります。
算数は「応用」部分が実に奥深いので教材開発が楽しめるところです。
算数ソフトで授業の進度が早くなったクラスは、こういう応用を楽しむ時間が生まれるので良いですね。
※２つの図は、岩波文庫の『塵劫記』に載っています。算数好きの先生にお勧めです。
－－
関連記事：