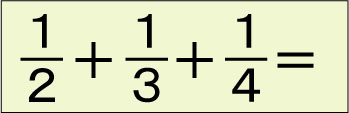【横山験也のちょっと一休み】№.2271
６月になりました。
楽しみです。
やるべきことは、進み続けることです。
■かけ算の筆算「たすきがけの法」■
１５世紀ごろのイタリア。
どうしたことか、計算熱が非常に高まったそうです。
数学史で有名人のルカス・パチオリという数学者が、かけ算のやり方を８種類も記録に残しています。
その中の一つに「たすきがけの法」があります。
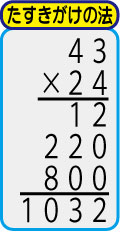
右の画像が、その方法を筆算形式で表したものです。
一寸考えると、やり方がだんだんわかってきます。
計算途中の１段目、「１２」は３×４でできているとわかります。
３段目の「８００」も４×２とわかります。
すると、残りの「２２０」も次第にわかってきます。
これを色別で整理すると、下のようになります。
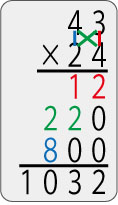２２の所は、４×４と３×２を合わせた数です。
このやり方は、少々ややこしいのですが、暗算の得意なインド人は「雷光の法」と呼んだそうです。
もし、時間があり、この計算を子ども達に紹介するとします。
その時には、「たすきがけの法」と表記して筆算を板書して、どうやって計算をしているのか考えさせるといいです。
原因（式）と結果（途中のやり方と答え）を見せる形になるので、その間の証明がとてもしやすくなります。
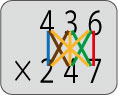子ども達がやり方を納得したら、３桁の「たすきがけの法」を考えさせてみましょう。
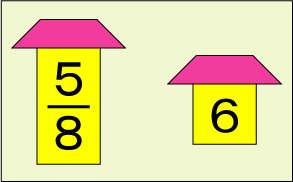
答えは右のようになります。
なかなか難しいですが、こういうことを考えるのは面白いですね。
※「たすきがけの法」については、『カジョリ初等数学史』に載っています。
—
こちらの2冊には面白い算数の授業が載っています。
「分数の紙」は、とにかくわかりやすい教材です。
算数を幅広く学んでみたいという先生にお薦めです。
この本に登場するネコちゃん、可愛いです。
 |
 |
—
関連記事：
