『遠山啓』は面白いですよ。
今日も一つ、グッと来たところを引用しましょう。
エンゲルスは弁証法の主法則として、“量と質との転化” “対立物の相互浸透” “否定の否定”という三つの法則を上げている。(p177)
頭の良い子はなぜすぐに分かり、そうでない子はなかなか分からないのか。
若い頃から、この極めて自然に現れてくる現象の原理がどうなっているのか、どう理屈づければ、この問いへの解答となるのか、と考えることがありました。
この疑問は、引用した「量と質の転化」の問題となって私の課題となっていました。
量をこなすことで、質的に変化していく。
その構造はいかなる様相をしているのか。
その答えとなりそうなことが、前回も引用したところに記されています。
それは質の差ではなく量の差に過ぎない(p241)
優れた見識です。
子どもの頭に質的な差があるのではなく、こなした量に差があるのだと言うことです。
量をこなせば、誰でも分かる!
遠山のこの言葉は、そういう命題を示しています。
これは、教師をやっていればそう願わずには居られません。
たくさん練習してできるようになる子。
少ない練習でできるようになる子。
そこにあるのは、量的な差だけと考えたいのが教師なのです。
と思っても、その差が大きくなってしまうと、心がくじけます。
どうにも質に差があるように思えてきます。
恐いのは、この瞬間です。
質に差があると見なしてしまうと、それはもうお手上げという感覚に襲われ、教育の無力さが頭を覆い始めます。
こういう落とし穴的思考にフタをして、「量の差とは何なのか」という問題意識を持っていると、出会うべき本に出会うようになります。
私の場合はデカルトの『精神指導の規則』でした。
尚それらすべを記憶して居らねばならないのである。この故に私は、一々を直感すると同時に他に移り行く一種の連続的な想像の運動によって、幾度もそれらを通覧するであろう。(p31、岩波文庫)
一つの事例を見ることで、その事例で何が起こったかが頭の中に入り、それを忘れない内に次の事例、さらに3つ目の事例をみること。
これができるのが頭のよい子で、2つ目、3つ目の事例に接する頃には1つ目の記憶が消えかけてしまうのが、そうでない子の頭の働きなのです。
よく、1時間で1問の問題を考えるタイプの授業があります。
これは、翌日まで、記憶の持続を求める学習になるので、そうでない子がアウトになるようにしむけている授業とも言えます。
大事なポイントは、忘れない内に次の事例を示ていく活動をすることです。
「短時間」がキーワードになります。
 こういう思いがあって、算数ソフトをつくりました。
こういう思いがあって、算数ソフトをつくりました。
ですので、私の作った算数ソフトは、その大方が理解の伴う類題を連続的に出題できる仕組みにしています。
短時間の内に類題を数問体験することこそが、遠山啓の言う「量の差」を克服する方法なのです。
このあたりのことを、御存命だったらお話ししてみたかったですね。
算数ソフトも見てもらいたかったですね。
--
関連記事:

ジョナサンの会。城ケ崎先生と川合先生のレポートから
【横山験也のちょっと一休み】№.3750 日曜日に「ジョナサンの会」が開催されました。 今回は、珍しく8人の参加で、過去最多となりました。 城ケ崎先生が鹿児島から戻ってきたので、再び司会を担ってもらいました。時間配分を気 …続きを読む

算数の話「論理的説明」と「感覚的説明」
【横山験也のちょっと一休み】№.3749 算数の話を一つ。 算数でわり算の筆算を学習するとき、「立てる→かける→ひく→おろす」という手順の説明がなされます。この手順は全くその通りで、この順に従って筆算を進めないと、正しく …続きを読む
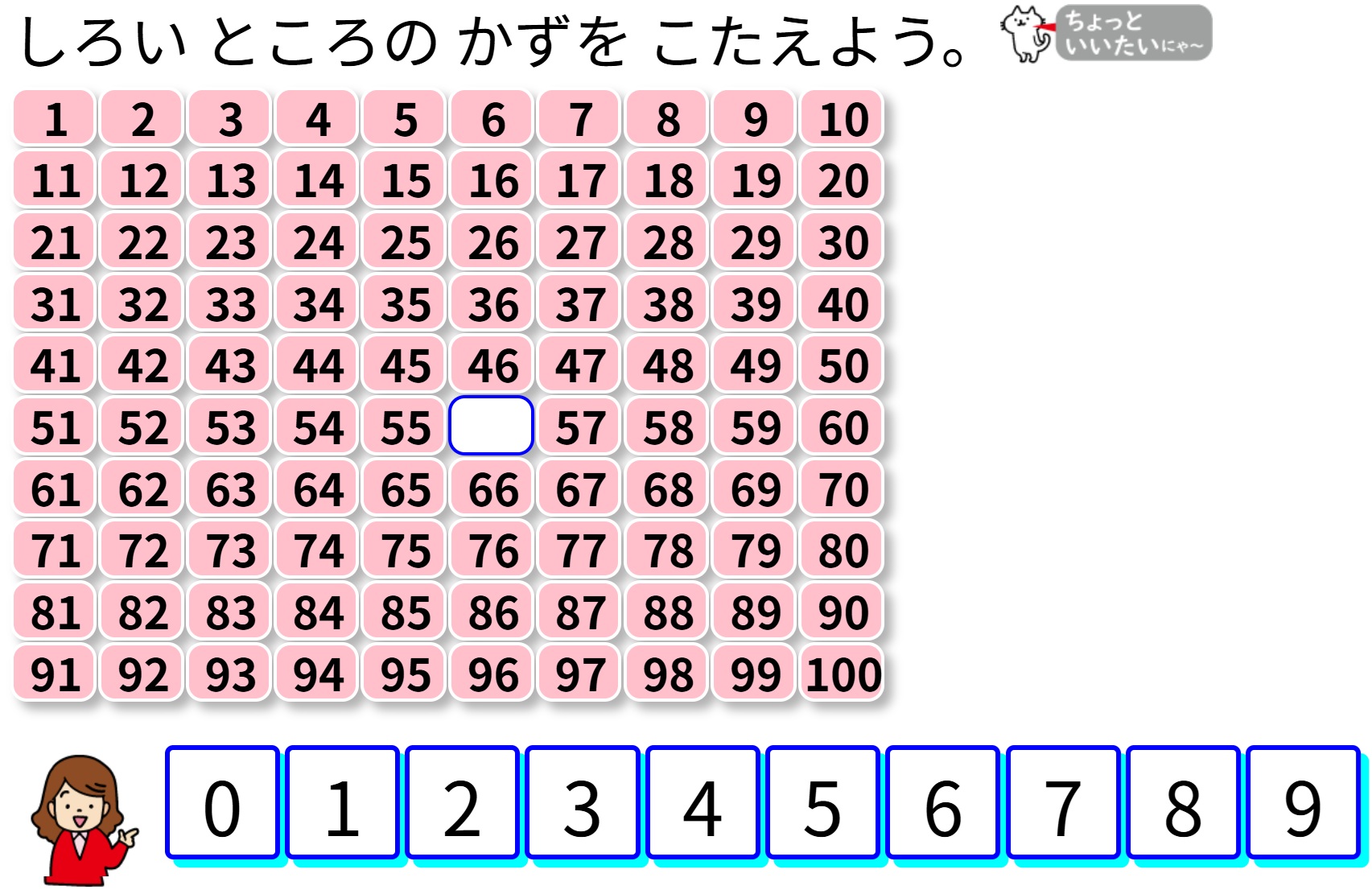
「さくらmathはじめます!」の100までの数!
【横山験也のちょっと一休み】№.3747 特別支援教育用の算数ICT教材「さくらmathはじめます!」から一つご紹介をします。 「100までの数」の単元用画面です。 当該ページを開くと、下のような「1~100までの数の表 …続きを読む
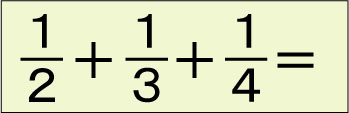
「1/2+1/3+1/4」を藤森良蔵の本と一緒に考える
【横山験也のちょっと一休み】№.3746 藤森良蔵の本に分数のたし算の問題とその考え方が出ていました。 この問題を見ると、たいていは2と3と4の最小公倍数(12)を考え通分して解いていきます。それも順当ないい方法なのです …続きを読む
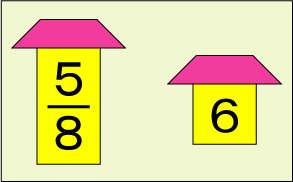
分数と家は似ている。という藤森良蔵はさすが!
【横山験也のちょっと一休み】№.3745 藤森良蔵の算術書が面白く、家に何冊かあります。 戦前に大活躍をした人で、算数系の通の先生はご存じと思います。 藤森先生の本(『算術学び方考え方と解き方』(山海堂出版部)に、分数の …続きを読む
